The concept that gravity arises from the warping of spacetime, rather than from an unseen force, is one of the most fascinating ideas in cosmology. Matter and energy influence the shape of space, dictating the trajectories of other masses within it. Instead of a direct line, the distance between two points is dictated by the curvature of spacetime itself.

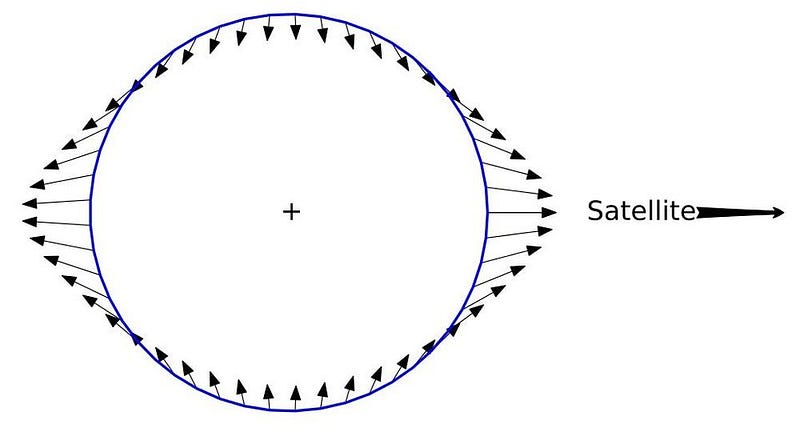
If you're searching for the most intensely curved regions of space, the best candidates would be black holes, where mass is densely packed into a small area. Interestingly, it's the smallest black holes that produce the most significant distortions in spacetime. Let's delve into this unexpected phenomenon.

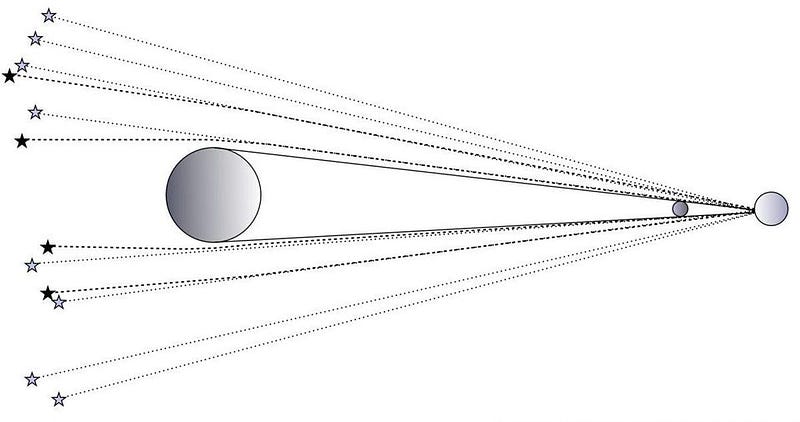
When we observe the cosmos on a grand scale, it often seems as though space is almost flat. Although mass can bend space and redirect light, even substantial concentrations of mass yield minimal light deflection. The 1919 solar eclipse was a landmark moment, as it demonstrated that light from distant stars was bent by the Sun's gravity, showing a deflection of less than one-thousandth of a degree, confirming General Relativity.

Gravitational lensing pushes this idea further, where massive objects like quasars or galaxy clusters can significantly warp space, creating distorted, magnified, and multiple images of background objects. Yet, even with trillions of solar masses, the effects are still only a fraction of a degree.

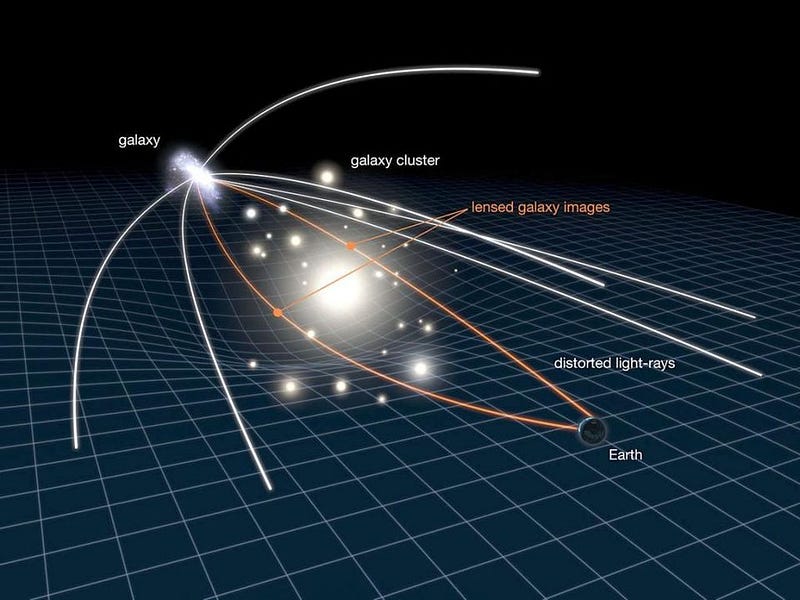
Crucially, it's not just proximity to a mass or the total mass that dictates the curvature of space; rather, it's the density of mass within a specific volume. For example, our Sun—considered a one-solar-mass object with a radius of about 700,000 kilometers—causes light to bend by approximately 0.0005 degrees at its edge.

Consider compressing the Sun into a smaller size: if it were reduced to the size of Earth, the light deflection would increase significantly, while a neutron star or a black hole would result in even greater deflection.

It’s crucial to understand that while the total mass remains constant across different scenarios—whether it's a Sun-like star, a white dwarf, a neutron star, or a black hole—the concentration of that mass is what intensifies spacetime curvature. If you maintain the same distance from the center of mass, the light deflection remains consistent at 0.0005 degrees, regardless of how compact the mass is.

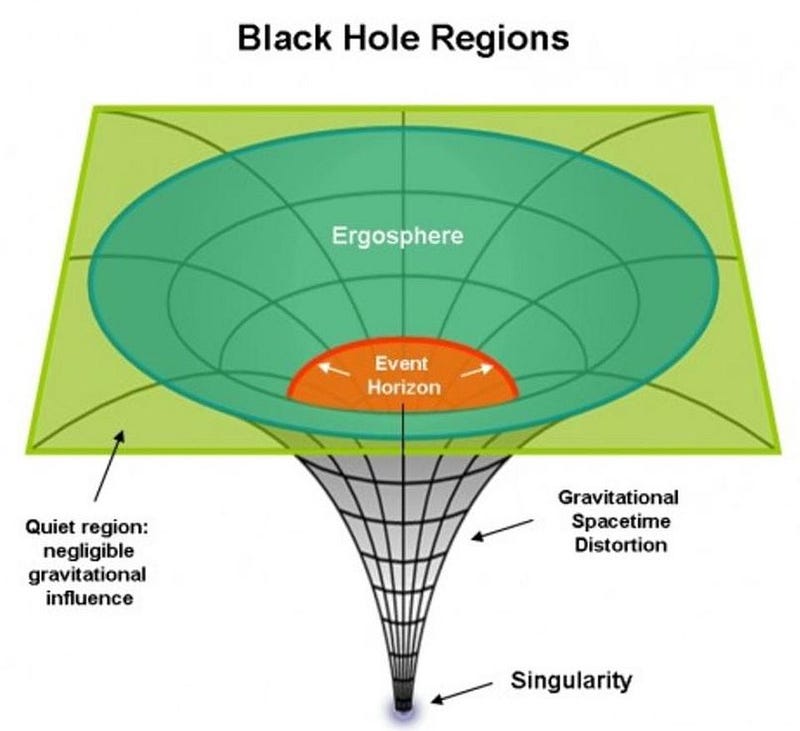
As you approach the most dense masses, such as black holes, the deflection of light becomes extreme, especially as it grazes the black hole's event horizon.

Despite having similar defining features like an event horizon—where escape velocity exceeds the speed of light—black holes vary significantly with mass. A larger black hole has a more extensive event horizon. Doubling the mass results in a doubling of the radius of this horizon, alongside similar scaling of escape velocity and light deflection.

However, not all characteristics scale uniformly across black holes of different masses. For instance, the tidal forces experienced while falling into a black hole can vary immensely. Approaching the event horizon of a black hole could lead to spaghettification, where the gravitational pull stretches you in one direction and compresses you in another.

Falling into the supermassive black hole at the center of M87 would generate only slight differences in force between your head and toes—less than 0.1% of Earth's gravity. Conversely, a fall into a solar-mass black hole would produce forces powerful enough to disintegrate atomic structures.

A particularly intriguing distinction between black holes of varying masses involves Hawking radiation, a phenomenon that has yet to be directly observed. All black holes emit a minuscule amount of low-energy radiation, which can be explained through quantum mechanics.

While popular illustrations depict particle-antiparticle pairs forming near a black hole, the reality is more nuanced. The quantum vacuum, where these particles emerge, differs in curved spaces compared to flat space. This variance in the quantum vacuum is what ultimately leads to Hawking radiation.

To observe the most intense Hawking radiation, one would seek out the smallest black holes, where the curvature at the event horizon is at its peak. In a comparison between a supermassive black hole and a black hole formed from our Sun, it becomes clear that:

• The larger black hole has a temperature billions of times lower.
• Its luminosity is about 20 orders of magnitude less.
• It will evaporate on timescales vastly longer—approximately 30 orders of magnitude.

Consequently, the least massive black holes in the Universe exhibit the strongest spatial curvature, making them invaluable laboratories for testing the principles of General Relativity.

Though it may seem paradoxical that the smallest black holes curve space more than the supermassive ones, this is indeed the case. The effective measurement of curvature is constrained by the event horizon, which is smallest around low-mass black holes. For phenomena like tidal forces or black hole evaporation, proximity to the singularity is more critical than mass itself.

Thus, the most promising sites for testing various aspects of General Relativity, and for exploring the earliest hints of quantum gravity, are around the smallest black holes, typically resulting from neutron stars merging into black holes with masses just 2.5 to 3 times that of the Sun. These smallest black holes, where space is most intensely bent, could hold the key to profound advancements in our comprehension of the Universe.

Starts With A Bang is now on Forbes, and republished on Medium on a 7-day delay. Ethan has authored two books, Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.