Unraveling the Tens Digit of a Massive Factorial Sum in Under a Minute
Written on
Chapter 1 Introduction to Factorials
The factorial of a whole number n, denoted as n!, is defined as the product of all positive integers up to n. For instance, 3! equals 3 × 2 × 1, which results in 6. In contrast, 2024! represents an extraordinarily large number!
Before proceeding, take a moment to think about the common characteristics among various factorials. I encourage you to pause here, grab a pen and paper, and give it a try. Once you're ready, continue reading for the solution!
Solution Overview
The critical insight for solving this large sum lies in recognizing that any number with factors of 100 will have a tens digit of zero!

Let’s use this knowledge effectively. Observe that larger factorials always encompass smaller ones. For example:
- 8! can be expressed as 8 × 7!
- 12! is equivalent to 12 × 11 × 10!
Now, for 10!, which expands to 10 × ... × 5 × ... × 2 × 1, it includes the following factors:

This indicates that all n! where n is less than 10 will contain a factor of 100. Consequently, we can ascertain the tens digit of this extensive sum by merely examining the initial factorials!

Mathematically, we can express this as follows:

Thus, we conclude:
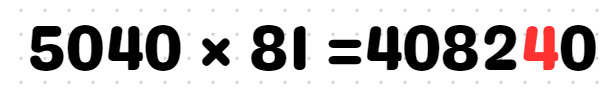
The tens digit we arrive at is 4! And that’s our final answer.
Reflection
What was your thought process during this puzzle? I'd love to hear your insights in the comments below!
If you enjoyed this challenge, consider sharing this collection of math puzzles on Medium:
Math Puzzles
Explore the best math puzzles on Medium, covering topics from Algebra to Calculus.
Thank you for taking the time to read! Please clap for this article if you found it informative.

If you appreciate my work, feel free to buy me a coffee as a gesture of support. Your kindness helps sustain my writing and personal endeavors.
Happy Solving, Bella