Chapter 1: Understanding the Problem

In this intriguing geometry problem, we focus on the center of a ball rather than the ball itself. Imagine a ball with a diameter of 4 units starting at point A and rolling along a track composed of three semicircular arcs with radii R1 = 100, R2 = 60, and R3 = 80. The ball maintains contact with the track without slipping. The challenge is to determine the distance traveled by the center of the ball from point A to point B.

Before diving into the solution, take a moment to visualize the scenario. Grab a pen and paper, and sketch the problem. Once you're ready, continue reading for the answer!

Section 1.1: Initial Considerations

To begin, we recognize that the radius of the ball is 2 units, derived from its diameter of 4. A diagram illustrating the situation will help clarify our next steps.

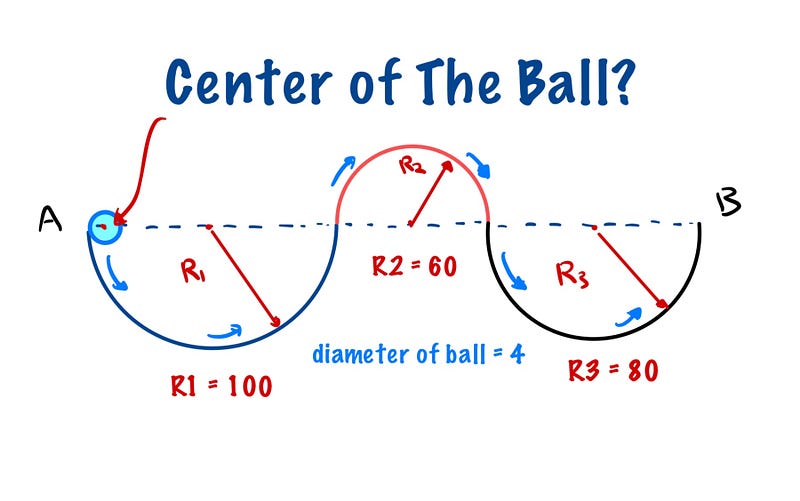
Now, let’s analyze what occurs as the ball rolls along the first semicircular arc. Imagine the path traced by the center of the ball, which forms another semicircle with a radius of 98 (100 - 2, since we subtract the radius of the ball).

This video explores the distance from a corner of a 50 ft square room to its center, paralleling our exploration of the ball's center.

Section 1.2: Tracing the Path

As the ball ascends the second arc, the center of the ball follows an outer path atop the track, which is crucial for our calculations.

When considering the semicircles traced by the ball's center, we find that the radii are as follows: 98 for the first arc, 62 for the second arc (60 + 2), and 78 for the third arc (80 - 2). With this information, we can now accurately compute the total distance traveled by the center.

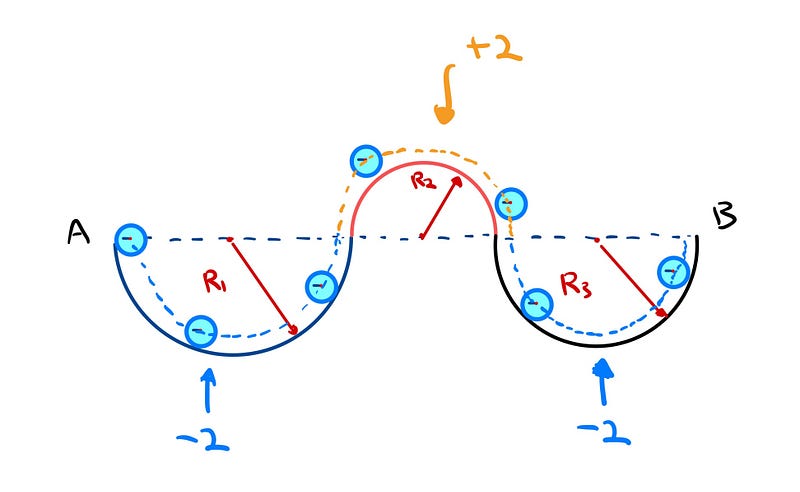
Chapter 2: Calculating the Distance

The distance traveled by the center of the ball can now be expressed mathematically. It’s fascinating how these geometric principles come together to yield a concrete answer!

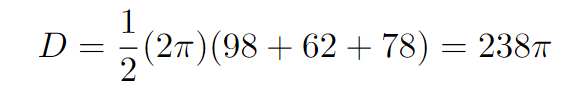
What insights did you gain from this problem? I’d love to hear your thoughts in the comments below!

This video demonstrates how to find the center of dilation, enhancing your understanding of geometric transformations.

Thank you for taking the time to read this exploration of geometry! If you enjoyed it, please show your support by clapping for the article. Your engagement means a lot!