By Stephon Alexander

As a theoretical physicist, my goal is to reconcile quantum theory with Einstein's Theory of General Relativity. While various frameworks like string theory and loop quantum gravity have been proposed, achieving a complete unification remains elusive.

Einstein's theory suggests that gravity is a result of the curvature of space and time. The sun warps the space around it, similar to how a person lying on a mattress causes it to sag. The orbits of planets, including Earth, follow the curved pathways formed by this distortion. This understanding provides vital clues about the essence of light.

While contemplating a drawing, I felt compelled to rethink my understanding of light.

Quantum mechanics presents a perplexing view of reality. For example, we perceive ourselves as occupying a specific location in space, yet a quantum particle explores all possible paths simultaneously, as though multiple copies coexist at once.

For years, I found myself hindered in my research, unable to achieve the breakthroughs I had envisioned. Quantum mechanics intricately involves the observer's role in its framework, yet integrating this aspect into a quantum spacetime has proven to be an immense challenge.

Last summer, an unexpected breakthrough occurred. Beth Jacobs, a member of the New York Academy of Sciences’ Board of Governors, invited me to her New York City apartment to meet the Oakes twins, artists known for their intricate drawings and innovative techniques. One of their works, Irwin Gardens at the Getty in Winter (2011), showcased a detailed depiction of the famous gardens designed by Robert Irwin at The Getty Museum in Los Angeles. The artwork was displayed against the backdrop of Central Park and the warm orange hues of the New York City skyline just before sunset.

This drawing ignited a spark in me to rethink the nature of light. I realized I should explore not just the physics of light but also how observers perceive this light information, which could lead to new principles for unifying quantum mechanics and relativity. My exploration of time perception and quantum uncertainty in the works of photographer Sam Heydt had already set the stage for this new perspective, and the Oakes twins provided the inspiration I needed.

Since childhood, Ryan and Trevor Oakes, now 35, have delved into the intersection of visual perception and light physics. After attending The Cooper Union for the Advancement of Science and Art in New York City, and years of experimentation, they developed a method to describe light information originating from a spherical surface.

Lawrence Weschler aptly summarizes their approach: in 2014, he curated a retrospective of the twins’ work at the National Museum of Mathematics in New York. He noted that they had achieved a remarkable breakthrough in depicting physical reality since the Renaissance, creating camera-obscura-like renderings on a concave grid without any optical instruments, relying solely on their unassisted vision.

Following my introduction to the Oakes brothers, I began to deeply investigate their work. The magic behind their art is a blend of experimentation, intuition, approximation, and technique, paralleling the work of leading physicists. They opened my eyes to the complex interplay between art and science and the potential for collaboration and dialogue between these fields. Both realms exploit techniques to uncover hidden realities, emphasizing secrets that are often overlooked.

The unique concave canvas they utilize to create their drawings fascinated me, particularly their circular approach to detailing. This reminded me of Van Gogh's technique in his later works, where the colors reflect light, evoking an almost extra dimension of textural depth. The shades can be perceived as three-dimensional data emerging from a two-dimensional surface. I was equally intrigued by the twins' use of embedded circles and the techniques that express this choice.

The Oakes brothers prompted me to consider "thought experiments," a method used by Einstein for elucidation. Their years of experimentation with visual perception have led them to insights about the physical nature of visual information.

In an email, they explained, “Our eyes can only capture light rays directed at them. Collectively, light rays converging onto a pupil spread radially, with each ray traveling perpendicular to an implied sphere's surface. The surrounding environment may be chaotic, but perceptually, we are at the center of a sphere of incoming photons conveying information about our surroundings.”

To embody this geometric perception, the twins create their art on a spherically concave surface rather than a traditional flat canvas. According to Trevor Oakes, using a concave surface aligns with the shape of light rays and makes more sense than a flat plane.

But how does the physics of light relate to the Oakes brothers’ discovery and technique? Quite a bit, as it turns out. Our exploration begins with James Clerk Maxwell’s 1860s revelation that electricity and magnetism are unified as electromagnetism, interdependent phenomena. This means that light is an electromagnetic wave composed of oscillating electric and magnetic fields traveling through space at light's speed.

The Oakes brothers have made me aware of the intricate connections between art and science.

Armed with this knowledge, a young Einstein envisioned a thought experiment: “If I chase a beam of light, I should observe it as an electromagnetic wave at rest, though spatially oscillating. Yet such a state seems unattainable.” This thought experiment relied on intuition, creativity, and a foundational understanding of physics.

Einstein imagined what the world would look like if he could catch up with a light wave. He concluded that he would perceive the electromagnetic wave as stationary. This scenario unveiled a paradox: Maxwell’s theory of light never allows for a light wave to be at rest. Resolving this paradox led to the development of relativity theory, establishing that light's speed remains constant, even if one were to nearly catch up to it. How could this be?

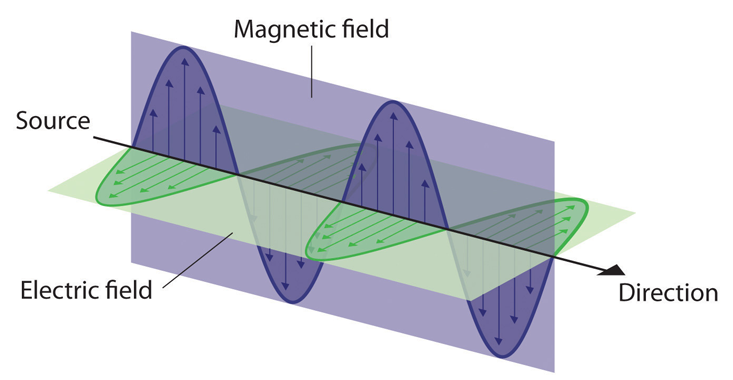
Einstein concluded that traveling at high speeds causes time to appear to slow down compared to someone at rest. Although it seems strange, it holds true. Even at speeds approaching that of light, time appears to move slower, meaning that light will still seem to travel at the same speed to an observer who remains stationary.

This realization reveals that space and time must be integrated into a unified four-dimensional spacetime continuum. Consequently, both time and space become relative, depending on one’s speed. Moreover, light does not exist separately in space and time; rather, it embodies a four-dimensional entity. In this framework, Einstein recognized that electric and magnetic fields are three-dimensional projections of a four-dimensional light wave, similar to how a two-dimensional shadow casts from a three-dimensional object.

This understanding clarifies the twins’ use of spheres. But we need one more analogy.

Imagine dropping stones into a pond. Each stone creates circular waves radiating outward from the point of impact. The water's surface is two-dimensional, resulting in circular wave patterns. A similar phenomenon occurs in three-dimensional environments when disturbances happen beneath the surface, creating waves that expand outward like a growing bubble.

What’s fascinating is that the twins arrived at similar insights through visual perception.

This physical description applies to light as well. Here, the stone corresponds to a source of light directed toward your eyes. As the twins correctly identified, light information emanates from the source as spherical light waves. But why does light adopt a spherical wave shape as it travels through space? This is where the four-dimensional spacetime perspective of light becomes crucial. My fascination grew with the twins’ technique, which experiments with their own perceptions and theoretical understanding of light's physics.

To grasp why light propagates as expanding spherical wave fronts from its source, we must consider Einstein’s theory of special relativity. Light traverses both space and time, and Einstein taught us that the structure of spacetime dictates how light behaves. Similar to how wind propels a sailboat, light navigates through the currents of spacetime. Einstein resolved his paradox about riding a light wave by merging space and time into a four-dimensional framework. We no longer reside at a point in three-dimensional space but within a point in four-dimensional spacetime. For instance, as you read this article, you occupy a specific three-dimensional location at a particular moment in time. Later, you will exist at a different point in four-dimensional spacetime.

This has implications for light. The figure below illustrates that light is not merely a point in space but a cone in spacetime.

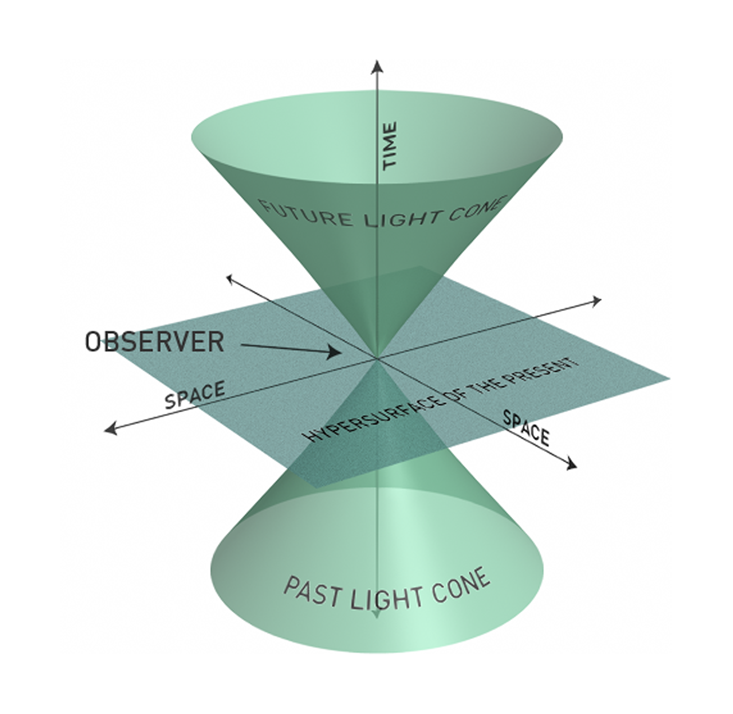
The origin, where time is zero, signifies the present. The cones above and below represent the future and past. No information can traverse outside the light cone, which corresponds to speeds exceeding that of light.

This accurately depicts light as it emerges from a point in spacetime and illustrates its trajectory to other points. The light traces a cone as time progresses toward the future. Tracing a single moment in time yields sequences of moving circular rings, akin to the spherical waves the twins incorporated into their creations. This explains why they pixelated their artwork Bond Street Terrace with circles.

A ray of light embodies four-dimensional spacetime. The equation for this light cone is well-known: X*² + *Y*² + *Z*²— *c*²*T² = 0. This equation is so elegant that it merits further discussion. The left side depends on three spatial dimensions (*X, Y, and Z), time (T), and the speed of light (C). Excluding time yields an equation for a three-dimensional surface. Including the time dimension transforms it into an equation representing a light cone, as illustrated above. Below, a computer-generated visualization shows spherical waves tracing the different points of the light cone emanating from its origin. The blue areas illustrate the time progression of these spherical waves.

It is remarkable that the twins arrived at such a profound aspect of physics—the spherical emanation of light—through the lens of perception alone. Equally astonishing is that they reached this understanding by developing their techniques through intuition and experimentation, mirroring the approach of a theoretical physicist seeking new truths.

The Oakes brothers’ work has illuminated the connection between quantum mechanics and gravity by emphasizing the deep relationship between spacetime, light, and observers. A precise framework for incorporating observers, whether conscious or not, into quantum gravity remains elusive. However, the twins reminded me of the importance of addressing this issue in my research. Witnessing artists like the Oakes brothers derive and apply physical insights through their experimentation and intuition reassures me that ongoing dialogues with artists could be the key to exploring uncharted conceptual territories, potentially leading to solutions as beautiful as the twins’ remarkable creations.