The Unusual Circle

The circle defined by a radius equal to the square root of 3 can be expressed by the following equation:

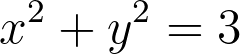
Let’s analyze the graph associated with this equation.

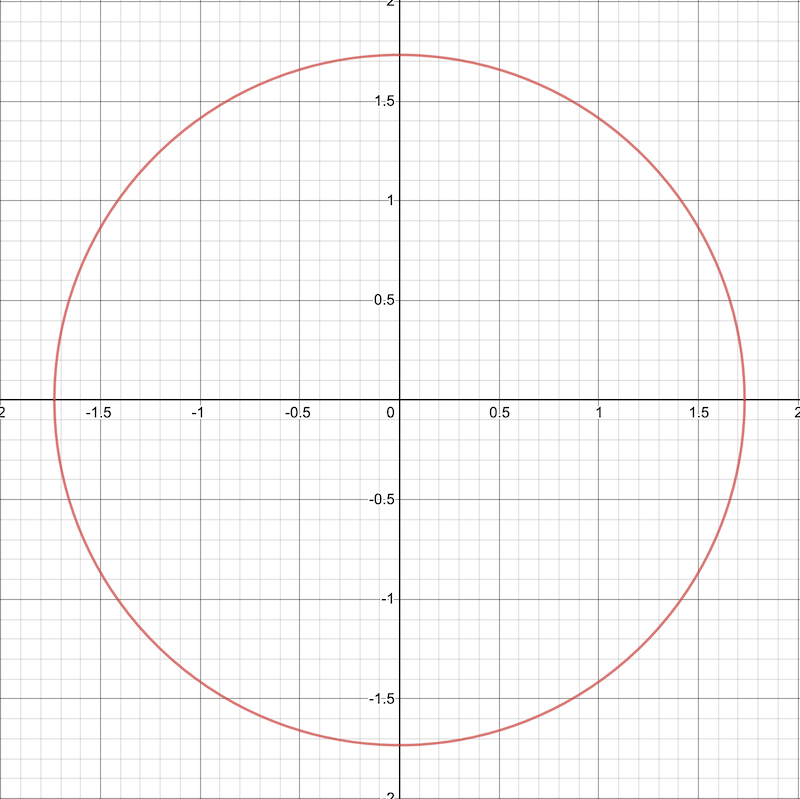
We understand that rational points are densely populated throughout the coordinate plane, meaning that between any two rational points, another rational point can always be found. Although the quantity of rational points is less than that of real points, there remains a significant abundance of them. Given this, it seems counterintuitive to believe that this quadratic curve does not intersect any rational points on the plane.

Now, let's formalize our inquiry: we aim to prove that there are no integers a, b, c, and d that satisfy the following equality:

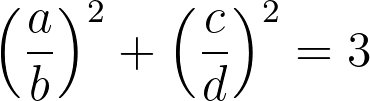
Additionally, it is necessary that the pairs (a, b) and (c, d) be coprime, implying that the fractions cannot be simplified further.

We will transform this equation involving rational numbers into an equivalent one that can be solved in integers, which will enable us to leverage the power of modular arithmetic discussed earlier.

Tricks with Divisibility

Let’s multiply this equation by a common denominator from the left side:

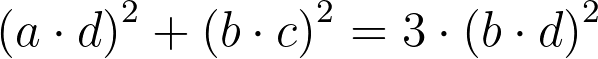
Post-multiplication, we can rearrange the terms by shifting the bc term to the right and factor out b² from the parentheses:

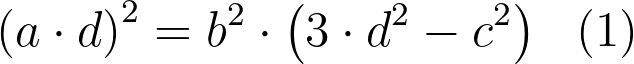
It becomes evident that b² must divide the right side of the equation, leading to the conclusion that it must also divide the left side. If b² divides (ad)², then b must divide ad:

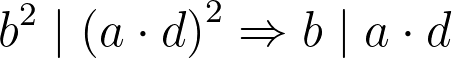
If b divides ad, we can express ad as the product of b and another integer z:

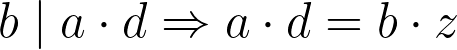
Now, let’s substitute bz into the equation as a replacement for ad and divide by b²:

Next, we can move c² to the left side:

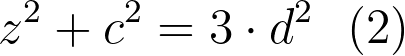
We have derived an equation in whole numbers. Given that c and d are coprime, we can leverage this information to demonstrate that the integer z must also be coprime to c and d.

Assuming a prime number p divides both z and c implies that p² divides both z² and c². Consequently, p² must also divide the left-hand side of the equations, meaning it should also divide the right side:

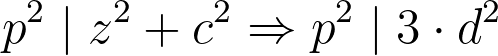
This leads to a contradiction, as the prime number p cannot divide d without implying that c and d are not coprime. Since p² cannot divide the prime number 3, we conclude that there are no primes p that can simultaneously divide z and c. A similar argument applies to demonstrate that no prime p can divide both z and d.

Modular Arithmetic Comes Into Play

We arrive at the following equation in whole numbers:

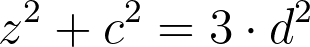
Knowing that z, c, and d are coprime suggests that at least two of these numbers must be odd. We will now convert the equation into terms of residue classes with modulo n equal to 4.

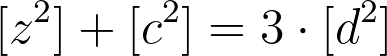
Assuming that d is odd, we find that the only possible value of [d²] is:

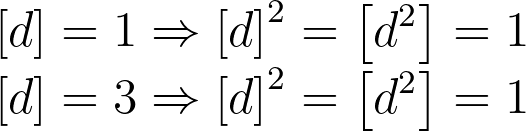
Multiplying this by 3 yields:

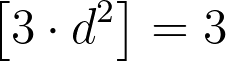
However, we previously established that it is impossible to find values for z and c such that:

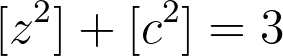
Thus, we reach a contradiction based on the assumption that d is odd.

Let’s shift our focus to assume that z is odd. This similarly implies that [z²] equals 1, like d, and we need to find suitable values for c and d such that:

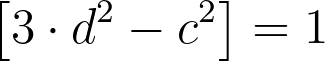
We can verify that this scenario is also impossible by examining all potential residue classes for d and c:

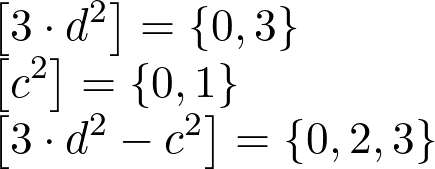
Thus, z cannot be odd either. This reasoning applies equally to c.

Ultimately, we have demonstrated that no whole number solutions satisfy the equation (2), which correlates to our initial assertion: there are no rational solutions to the equation:

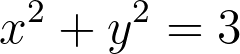
Further Questions

In this article, we validated that only two categories of circles exist centered at the origin. However, what can we deduce about circles in general?

Should we formulate a theorem applicable to every circle with an irrational radius centered at the origin? Or might we employ a generalized theory to explore this? Will our findings regarding the two types of circles extend to all circles on the coordinate plane? Could we uncover circles with merely one or two rational points?

Is it feasible to develop a similar theory when transitioning from circles to conics? Or does that complicate our understanding of how many points such conics may possess?

Numerous inquiries remain, but it's impractical to address all of them in a single article. I plan to tackle many of these questions in upcoming articles, and I hope you found this exploration engaging and are eager for more insights in this series.

Discover the hidden aspects of the circle of life and how to unlock its mysteries through rotation.

Delve into the esoteric nature of circles and uncover the hidden life that they embody.