A Unique Integral Expression for the nth Derivative with Applications
Written on
Chapter 1: Introduction to the Integral Formula
About a year ago, I embarked on a quest to derive a different formula for the nth Fibonacci number, one that deviates from Binet's classic equation. While experimenting with the generating function, I pondered methods to isolate the coefficients without needing to differentiate the function multiple times.
This narrative outlines the findings from my exploration. We will derive and demonstrate this result, which can be utilized to tackle interesting problems and potentially validate other mathematical theorems.
This article presents an elegant formula for calculating derivatives without performing any differentiation. For those familiar with complex analysis, think of how this relates to Cauchy's integral formula for derivatives.
Moreover, this formula will provide a means to compute the nth Taylor coefficient, which I will present as a corollary. As we will discover, this corollary proves to be quite beneficial.
Feel free to navigate to any section of interest:
- The Theorem
- Proof of the Theorem
- The Trivial Case
- A Constant Function
- A Monomial
- The Corollary
- A Formula for the nth Fibonacci Number
The Theorem
The following statement applies to most functions encountered in analysis and calculus.
Before delving into the proof, we require a preliminary lemma.
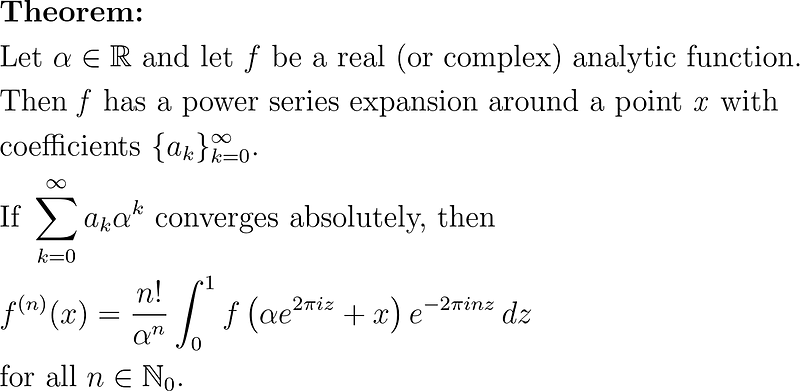
The lemma provides a useful indicator function, which we will repeatedly utilize.
Proof of the Theorem
We can now proceed to demonstrate the theorem.

Notice how we cleverly removed the summation using the lemma. This is feasible due to the convergence of the series, allowing us to apply the distributive property to the infinite series. According to the lemma, the only term for which the integral does not yield zero is the nth term, which we can obtain by rearranging the components.
It’s important to highlight that any real analytic function within an open set D on the real line can be extended to a complex analytic function in an open set of the complex plane that encompasses D. Thus, the assumption of the function being "real or complex" is valid, provided we extend the function to evaluate it at complex numbers.
The Trivial Case
A particularly interesting outcome that emerges directly from this theorem is:
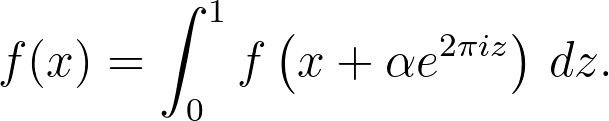
Despite appearing to integrate f around a circle of radius r centered at x, caution is warranted. When conducting contour integration along a parameterized curve, we must multiply by the derivative of the parameterization and evaluate the integral of f along that curve. Hence, we cannot immediately invoke Cauchy's theorem.
However, we can indeed apply Cauchy's integral formula. Let’s prove this.
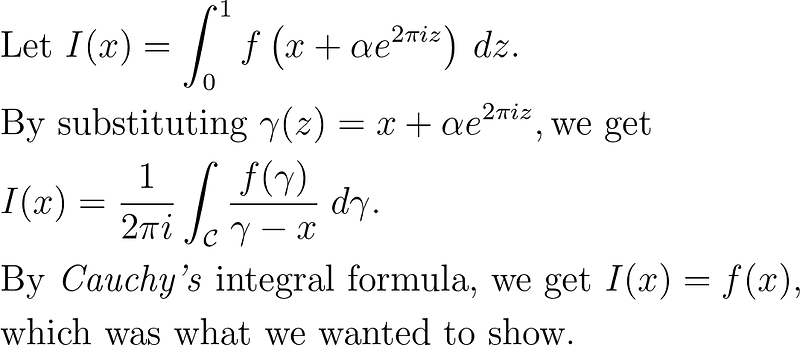
A Constant Function
Now, let's examine f(x) = c for some constant c.
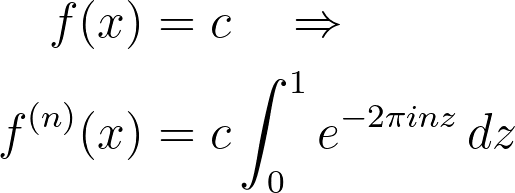
The lemma assists in ensuring that we obtain zero if n ≠ 1 and c if n = 0. We proved the latter in the previous section.
A Monomial
Next, we will utilize the binomial theorem to derive the nth derivative of a monomial.
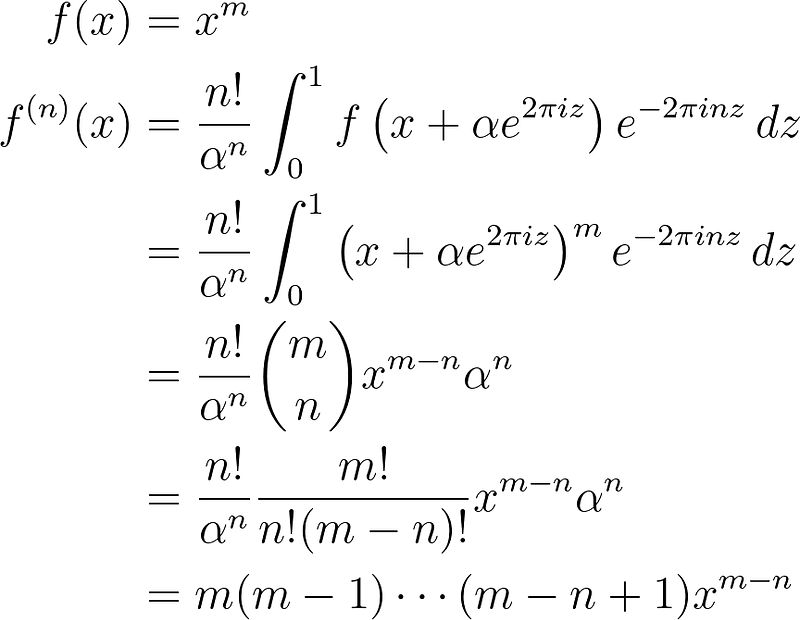
Observe that the lemma extracts the nth term from the binomial sum. In particular, if we consider the special case where n = 1, we arrive at the familiar result of mx^(m-1).
The Corollary
By dividing both sides of the theorem's formula by n!, we can derive the nth Taylor coefficient, leading to the following corollary.
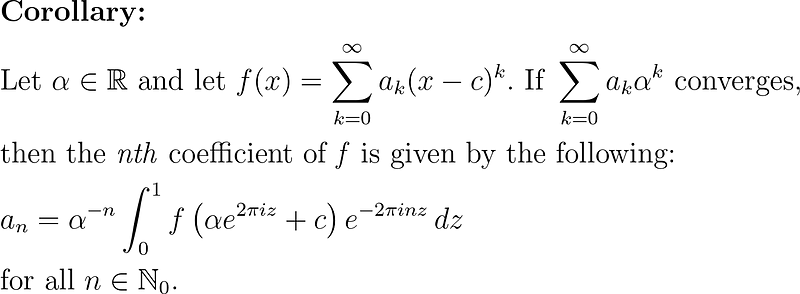
The proof of this corollary is straightforward. We simply apply the theorem and divide by n!, yielding the nth Taylor coefficient on the left-hand side.
A Formula for the nth Fibonacci Number
It is widely recognized that the generating function for the Fibonacci sequence can be expressed as:
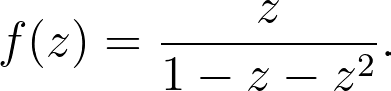
While it is possible to represent it with a 1 in the numerator instead of z, this is merely a matter of indexing. For our purposes, we will begin at 0, so the (n+1)-th term of its Taylor polynomial corresponds to the nth Fibonacci number.
Utilizing the corollary, we can extract the coefficients, presenting us with yet another formula for these renowned numbers. However, we need to be cautious. The corollary is applicable only if:
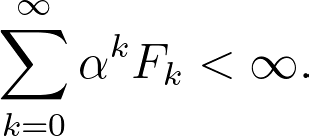
The Fibonacci numbers grow approximately in alignment with the exponential function, using the golden ratio φ as its base:
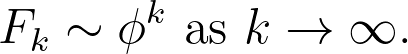
Therefore, the corollary holds for φ < 1. Assuming c = 0, we arrive at our formula:
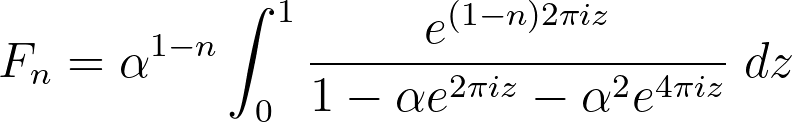
This is valid for all φ < 1. You might want to try φ = 1/2 for instance. For n = 9, we should derive 34. You can verify this result. Note that while a small non-zero imaginary component might appear, it is likely a rounding error from Wolfram’s algorithm.
Thus, we can effectively utilize this method to extract coefficients from Taylor series, proving to be a valuable tool in conjunction with the theory of generating functions.
If you have any inquiries, suggestions, or feedback regarding this article, please feel free to connect with me on LinkedIn.
Kasper Müller - Senior Consultant, Data and Analytics, FS, Technology Consulting - EY | LinkedIn
Programming, mathematics, and education are among my primary passions. My interests also encompass data science and mathematical modeling.
In this video, you'll learn how to derive a formula for the nth derivative of f(x) = e^(kx), providing a solid foundation for understanding this beautiful integral formula.
This video discusses how to find a formula for the nth derivative of the function f(x) = x^n, offering insights into series and their applications.