Vector Norms Explained

Vector norms represent various methods for quantifying the magnitude of a vector. Consider a linear regression scenario with a single feature, ?1. This situation presents two parameters: ?0 (the intercept) and ?1, both assigned a value of 1. The parameters can be represented within a 2-dimensional vector, ?:

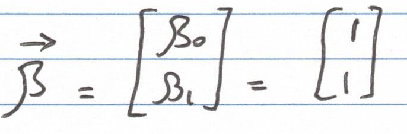
For a comprehensive review of linear algebra concepts, check out:

An overview of linear algebra concepts for machine learning

L2 Norm: The Euclidean Measure

The L2 norm, commonly referred to as the Euclidean norm, is the most prevalent method for assessing a vector's magnitude. It calculates the distance from the origin to the vector's endpoint, akin to determining the hypotenuse's length in a right triangle using the Pythagorean theorem.

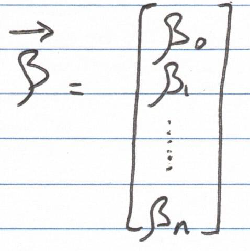
To compute the L2 norm for the aforementioned n-dimensional vector, we apply the following formula:

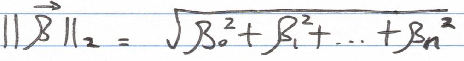
The notation for the L2 norm consists of double bars surrounding the vector name, accompanied by the subscript 2. For our 2-dimensional parameter vector ?, where both ?0 and ?1 are set to 1, the L2 norm becomes:

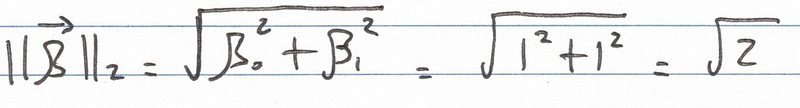
The distance from the origin to this vector, or its L2 norm, equals the square root of 2. Plotting all vectors with an L2 norm of the square root of 2 generates a circle with a radius of the same value.

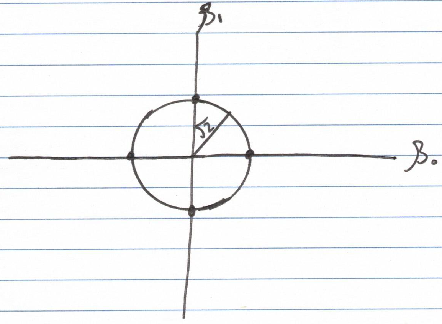
This aligns with the equation for a circle centered at the origin:

a² + b² = c², where c represents the radius.

L1 Norm: The Manhattan Measure

Another method for determining a vector's magnitude is through the L1 norm, also known as the Manhattan norm.

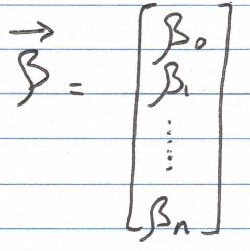
To calculate the L1 norm of an n-dimensional vector, we sum the absolute values of all vector components as follows:

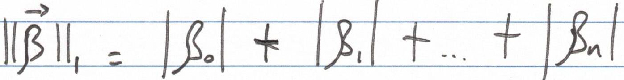
The notation for the L1 norm also features double bars surrounding the vector name, along with the subscript 1. Hence, for our 2-dimensional parameter vector ?, with both parameters set to 1, the L1 norm results in:

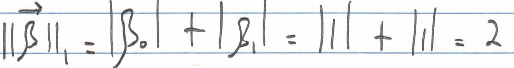
As demonstrated earlier, the L1 norm totals 2. When we visualize all vectors with an L1 norm of 2, they form a diamond shape.

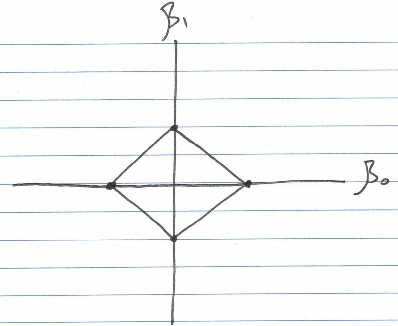
Understanding the Connection between L1/L2 Norms and Regularization

Regularization is a strategy aimed at minimizing overfitting. In scenarios with low bias, where the model excessively adapts to the training data, variance becomes elevated due to the bias-variance tradeoff. Regularization methods, including L1 and L2 regularization, help simplify model complexity, thereby curtailing overfitting.

In ordinary least squares (OLS) regression, the goal is to minimize the square of the residuals:

The sum of squares effectively represents the L2 norm squared of the residuals. In regularized regression, a penalty term is incorporated into the cost function, imposing a constraint. This can involve constraining the L1 norm of the parameters vector (as seen in L1 or lasso regression) or constraining the L2 norm (as in L2 or ridge regression). This explains the terminology of L1 and L2 regularization.

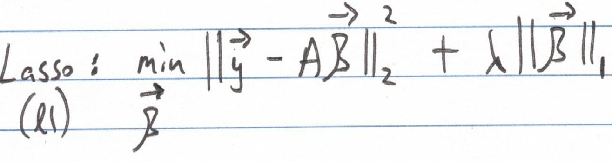
In L1 regression (lasso regression), the goal is to keep the L1 norm of the parameters vector within a specified limit. In essence, we aim to minimize the cost function while ensuring that the L1 norm does not exceed a designated threshold. As previously noted, plotting all vectors corresponding to a particular L1 norm value results in a diamond shape.

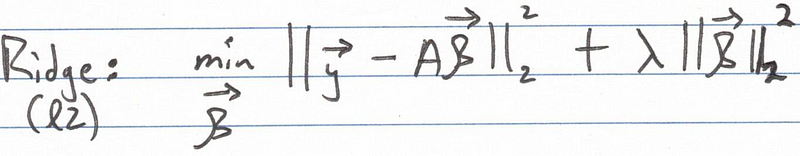
Conversely, in L2 regularization, the objective is to keep the L2 norm of the parameters vector at or below a certain threshold. Thus, the parameters vector must lie on or within the circle illustrated earlier.

Note: L1 and L2 regularization techniques are not advisable when only two parameters are present. This discussion aims to provide a brief, intuitive understanding of how these techniques relate to the L1 and L2 norms.

Understanding Vector Norms in Machine Learning: This video delves into L1 and L2 norms, unit balls, and their application in NumPy for practical understanding.

When Should You Use L1/L2 Regularization?: This video explains the scenarios in which L1 and L2 regularization should be applied in machine learning models.

In conclusion, grasping the concepts of L1 and L2 norms is essential for a deeper understanding of what L1 and L2 regularization aim to achieve. Thank you for engaging with this material!