The Act of Counting

Where does the idea of "number" emerge in our daily experiences? The core activity of counting is where numbers manifest, stemming from our innate sense of quantity. While counting, we select a standard item (e.g., an apple) and quantitatively compare it to a collection of similar items (e.g., a basket of apples).

The term used for a collection of individual items, such as a crowd of people or a basket of apples, is "multitude." A multitude consists of discrete objects, which differ from continuous properties like height and area. When evaluating whether an object is an "apple," we are dealing with a qualitative attribute. For each item in the multitude (the basket), we ask: is this an apple? If the answer is "yes," we increment our count; if "no," we continue to the next item without adjusting the count.

The numbers we utilize for counting are whole numbers (0, 1, 2, 3…), which means they are not composed of parts. Whole numbers are used to count distinct items that are separate from one another. The quantitative relationship between our standard (the apple) and the multitude being counted (the basket of apples) is the number itself. This relationship specifies a quantity—the number of times our standard appears in the multitude.

If we modify our unit, the resulting number changes. Instead of counting a single apple, we could count pairs of apples, yielding a different total even when the multitude remains constant.

Measuring and Counting

When we count, we employ a qualitative standard to establish the size of a multitude, where the count reflects the repetitions of our standard within that multitude—for example, ten apples in the basket.

A magnitude, such as height or area, is both quantitative and continuous. Can we count magnitudes in the same manner we count multitudes? The answer is no; magnitudes and multitudes are inherently distinct.

Magnitudes are continuous, whereas multitudes consist of individual items. While we can count discrete objects, magnitudes do not have distinct components—only a continuum. So, what is our approach? We establish a quantitative standard from a magnitude of the same type, known as a unit. This unit allows us to compare the sizes of similar magnitudes by counting how many times the unit fits within the magnitude—a process termed measurement.

For instance, when measuring a person's height with a meter stick, the meter stick serves as our unit and possesses its own height, thus being a magnitude of the same type. We then count how many times we can place the meter stick against the person—say, two times—resulting in a height of two meters.

Indeed, measurement incorporates counting, but it involves counting a unit against individual magnitudes rather than increasing a count based on a qualitative comparison to a standard, as in counting multitudes.

Ratios: A Comparison of Magnitudes and Multitudes

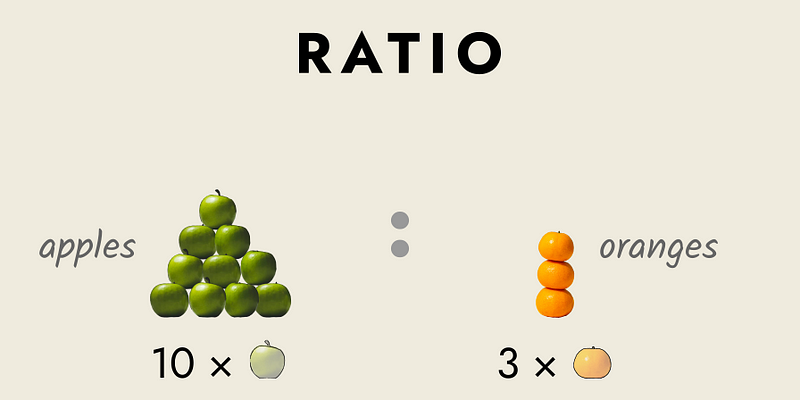
When measuring magnitudes, we conduct a quantitative comparison between one magnitude (what we are measuring) and another (our measuring unit). Any quantitative relationship between items, focusing on their relative sizes, is referred to as a ratio. Ratios are expressed in the format ? : ?, for example, "10 apples : 3 oranges," read as "10 apples to 3 oranges."

Ratios can compare magnitudes, multitudes, or even numbers themselves. For instance, consider the ratio of a man's height to a two-foot ruler: "6 ft : 2 ft." Unlike numbers, which are limited to comparisons between two entities (the unit and the item being counted or measured), ratios can encompass an unlimited number of comparisons, such as "10 apples : 2 oranges : 6 lemons : …" and so forth.

Consequently, only ratios involving two items can result in a number in the context we are discussing. This number is ascertained once the process of measurement (for magnitudes) or counting (for multitudes) concludes.

For counting, the process wraps up when every individual item in a multitude has been evaluated against our standard, incrementing the total each time we confirm an item meets the criteria—"Yes, this is an apple; add ‘1’ to the total."

And when is a measurement considered complete?

Measurement concludes when we count how many times the unit (like a ruler) fits into the magnitude being assessed (like the man's height). We then record a number that captures the quantitative relationship between the magnitude and our unit.

However, in many cases, a magnitude cannot be counted using whole numbers as individuals in a multitude can. A person's height may not precisely be five or six feet but rather a value in-between. In such instances, whole numbers fall short for measurement, as they count distinct, individual items, while height exists within a continuous range.

Rational Numbers and Fractions

Since magnitudes can possess a variety of values that lie between whole numbers (1, 2, 3…), we need to break down whole numbers into smaller segments, allowing us to encompass a broader range of values.

This is where fractions come into play—equal subdivisions of our original unit. For example, one foot can be divided into twelve inches, where one inch can be expressed as the fraction 1/12 ft, and two inches as 2/12 ft.

By utilizing a combination of feet and inches, we can "count off" a person's height, perhaps finding they are 5 ft 7 in. tall, read as "five feet, seven inches." This measurement can also be represented entirely in feet as 5 7/12 ft.

The notation "5 7/12" represents a new type of number, a rational number—a comparison between whole numbers that enables us to count the (potentially fractional) number of units within a magnitude. The format "5 7/12" is known as a "mixed number," as it combines different units (feet and inches). Traditionally, this was how measurements were recorded; contemporary scientific measurements often utilize decimal notation.

The height of 5 7/12 ft can be expressed entirely in inches, i.e., 67/12 ft, represented as an "improper fraction" (where the numerator exceeds the denominator).

In general, rational numbers are expressed in the form of fractions, i.e., a/b, where a and b are whole numbers, and b is not zero. It is crucial to note that rational numbers are not merely fractions; they can be presented in fractional form.

For instance, the rational number represented by the fraction 7/12 can also be expressed in decimal format as 0.583..., with a vinculum over the numeral "3" indicating it repeats indefinitely.

I conceptualize fractions as literal subdivisions of a unit, as individual components of a larger unit. If you possess seven inches, you have seven subdivisions of a foot, with each subdivision being 1/12 of a foot. In this regard, fractions represent multitudes (groups of items).

Conversely, rational numbers illustrate quantitative relationships between entities—they are neither multitudes like fractions nor magnitudes like lengths. Confusingly, the fractional format a/b can also depict magnitudes, such as a continuous length. Instead of seven distinct inches lined up, we could have a short length expressed as 7/12 ft, which is similarly expressed in decimal as 0.583 ft.

This flexible application of fractional notation is a topic I plan to explore further in the future. Thus, rational numbers describe both multitudes and magnitudes, and regardless of their format—fractional or decimal—they remain rational numbers, signifying a relationship between whole numbers.

It’s worth noting that the term "rational" does not derive from "ratio," despite their similarities. In this context, rational means "not irrational." The term "irrational" in mathematics refers to numbers that cannot be precisely defined—unlike rational numbers, which can be completely specified as a ratio of whole numbers. We will delve deeper into irrational numbers in subsequent discussions.

Key Takeaways

• A number represents a quantitative relationship between an item and a unit (a standard used for comparison).
• Quantity exists in both multitudes (groups of individual items, such as a crowd) and magnitudes (continuous attributes, like height and length).
• We count individuals in a multitude and measure magnitudes against another magnitude of the same type (serving as our unit).
• A ratio signifies any quantitative comparison between entities, formatted as ? : ?. Ratios can compare an unlimited number of entities simultaneously but yield a number only when comparing two entities.
• A fraction represents a subdivision of a unit into equally sized smaller parts. Fractions are essential since real-world measurements rarely align with whole units.

And follow/subscribe here on Medium to receive new articles from Reduct as they are published!