Exploring the Intersection of Projective Geometry and Information Theory
Written on
Chapter 1: The Mars Mission
To grasp the intersection of projective geometry and information theory, let's consider a specific scenario. Picture yourself overseeing a research expedition on Mars, where you've successfully landed your spacecraft on the Martian surface.
As your drone sets out towards Mount Olympus, the highest peak on Mars, you quickly realize there's an issue with its path. If it continues, a collision with a rock could lead to severe damage.
To avert disaster, you must promptly send a corrective signal from mission control on Earth to your drone on Mars. However, the vast distance presents a significant challenge: signal noise can distort your transmission, leading to potential errors.
Your goal is to ensure that the Mars drone receives the correct instructions without fail. How can you tackle this challenge?
Section 1.1: Cosmic Radiation and Signal Integrity
Most signal noise arises from cosmic radiation. Initially, researchers attempted to solve this issue with equipment designed to filter out such interference.

This approach changed dramatically when a young master's student, Claude Elwood Shannon, introduced groundbreaking ideas in his thesis titled “A Symbolic Analysis of Relay and Switching Circuits.” His 1948 paper, “A Mathematical Theory of Communication,” laid the foundation for the field we now call information theory.
Section 1.2: Understanding Error Detection
A signal can be viewed as a series of binary bits—zeroes and ones. Let's assume the corrective signal you intend to send is:
10101
If cosmic radiation alters one bit, the outcome might appear as:
11101
While it may seem like a minor change, it could result in a catastrophic failure for your Mars drone. To mitigate this risk, you could duplicate each bit in pairs:
10101 ➔ 11 00 11 00 11
In this revised signal, the drone anticipates receiving two identical bits per block. If a cosmic ray flips one bit, the signal might read:
11 01 11 00 11
Although the second block becomes unreadable, the drone recognizes that an error has occurred. This marks a significant evolution from merely transmitting information to incorporating error detection.
The brilliance of Shannon lies in his ability to build upon this idea further.
Subsection 1.2.1: Advancing to Error Correction
Shannon pondered, “What if we encode three identical bits for each segment?” The intended transmission might then look like this:
111 000 111 000 111
If cosmic interference alters one of the bits, you could receive:
111 010 111 000 111
The drone could deduce that the second block likely consisted of three identical zeroes because of the low probability of cosmic interference. While this isn't foolproof, it represents progress in error-correcting code.
However, this method comes with a cost: the amount of information transmitted triples. Shannon discovered that to increase error resistance, the speed of transmission decreases due to added redundancies. He identified the limits of this process, which he termed the channel capacity. Remarkably, he found that even random codes can exhibit self-correcting properties.
Section 1.3: The Hamming Code
In collaboration with Richard Hamming at Bell Labs, Shannon explored innovative solutions. Hamming faced the unique challenge of working with a mechanical relay computer that was often unavailable on weekends. Frustrated by delays, he devised what we now recognize as the Hamming code.
This code encodes each three-bit combination into a seven-bit string:
000 ➔ 0000000
001 ➔ 0010111
010 ➔ 0101011
011 ➔ 0111100
101 ➔ 1011010
110 ➔ 1100110
100 ➔ 1001101
111 ➔ 1110001
This transformation allows you to apply the Hamming code to your corrective transmission as follows:
10101 ➔ 010 101 ➔ 0101011 1011010
Although seemingly arbitrary, the Hamming code provides the same error-correcting capabilities as the tripling method, with a better redundancy-to-information ratio of 2.33.
Chapter 2: The Fano Plane and Its Significance
To comprehend how the Hamming code operates, we must explore a specific projective geometry known as the Fano Plane.
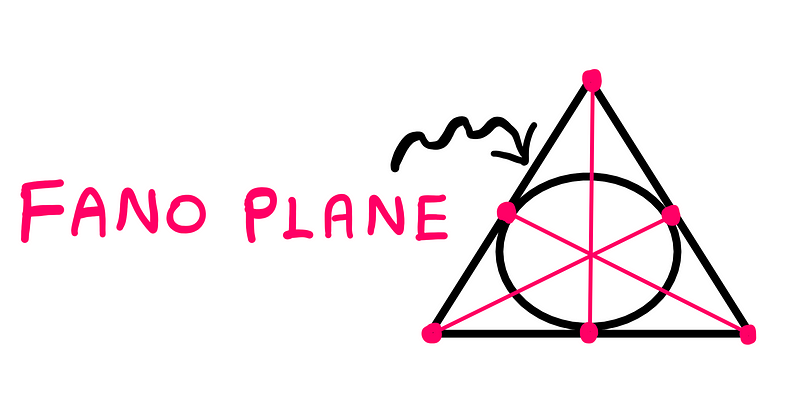
Developed by mathematician Gino Fano, the Fano Plane consists of seven points and seven lines. At first glance, it may appear that there are only six lines. However, the seventh line is curved, demonstrating the unique properties of projective geometry.
The governing axioms of projective geometry state:
- Every pair of points creates a unique line.
- Every pair of lines intersects at precisely one point.
The Fano Plane adheres to these axioms, allowing the curved line to be indistinguishable from a straight line.
In this video, "Projective geometry | Math History | NJ Wildberger," the relationship between projective geometry and its historical context is explored, providing a deeper understanding of these mathematical principles.
Section 2.1: Bridging Geometry and Error Correction
You might wonder how the Fano Plane relates to the Hamming code or the Mars drone. They are conceptually intertwined, but this connection is intricate and requires further exploration, which will be addressed in the next part of this series.
Closing Remarks
Before concluding, it's worth noting the significant advancements stemming from error-correcting codes. The Hamming code sparked a wave of innovations in error correction technology.
For instance, the Reed-Solomon code enables CDs to remain functional despite scratches, while modern flash drives utilize the Bose-Chaudhuri-Hocquenghem code to combat data corruption. The applications for these technologies extend from Mars rovers to banking systems.
As for your Mars drone, can you devise an error-free transmission in time to alter its course and avert disaster?
I apologize for leaving you on a cliffhanger, but we'll uncover the resolution in the next installment of this essay series. Thank you for joining me on this exploration!
The second video, "FPG6 Fundamental Theorem of Projective Geometry Proof - YouTube," delves into the fundamental theorem of projective geometry, enriching your understanding of the mathematical concepts discussed.