Introduction to Non-Calculator Math Questions

While preparing for a beginner's training session, I sought out some intriguing non-calculator Olympiad problems. I found four compelling questions that primarily rely on basic mathematical manipulation techniques. Mastering these tricks can significantly enhance our problem-solving skills.

Here are the four questions for you to explore:

1. Solve for all x such that

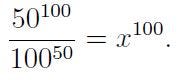
2. Determine which value is greater:

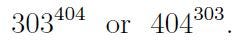
3. Calculate the value of x when x = 45678³ - 45676³:

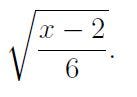
4. Find all x that satisfy:

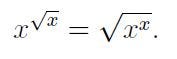
As always, I encourage you to attempt these problems before reviewing the solutions. Remember, the aim is to solve them without a calculator.

Solutions Overview

1. The first problem can be approached in a couple of ways. Here’s one method:

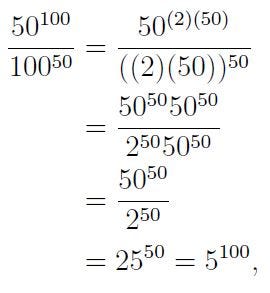
We find that x = 5. Alternatively, if we recognize the equation's form, we could also derive:

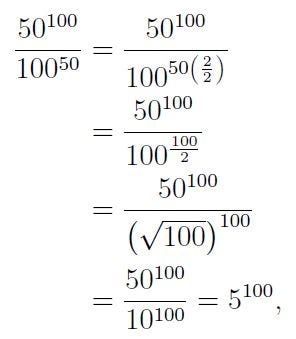
Again, we arrive at x = 5. Note that, as pointed out by Evaggeloskaravias, we could consider the square root of 100 to yield -10, leading to two solutions: 5 and -5.

2. In this task, our objective is to analyze the numbers 303^3 and 404^3 to identify common factors, which will help us compare them effectively. Immediately, we can see that both expressions share 101 as a factor. Let's break it down further:

From this, it becomes evident which number is larger. Surprisingly, 303^3 is significantly greater than 404^3, exceeding it by more than 101^3 times.

3. We define a = 45676, allowing us to express x as follows:

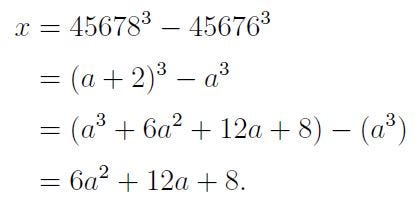
This leads us to conclude:

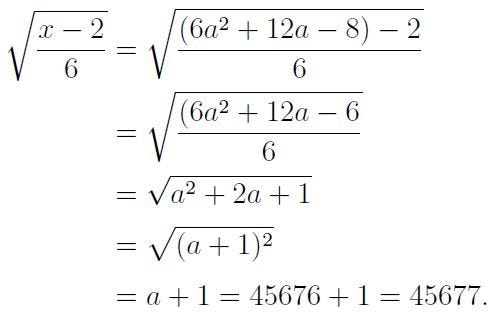
We could also define a = 45678 to reach the same result.

4. For the final problem:

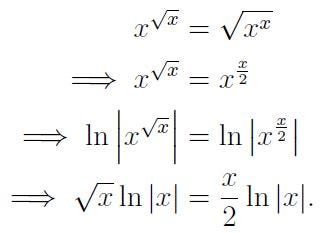
It's important to note that using the natural logarithm is not critical; any logarithm base will suffice since we exploit the properties that allow us to simplify exponents. Continuing:

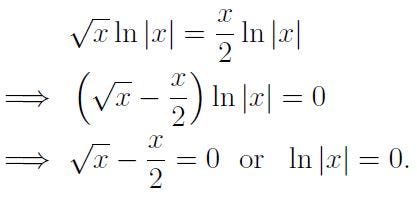
Let’s evaluate these separately. First,

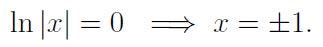
And secondly,

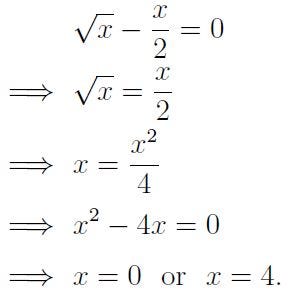
We have identified four potential solutions: x = -1, 0, 1, and 4. Let’s verify each in the original equation:

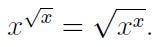
After checking, we find that x = -1 does not satisfy the equation.

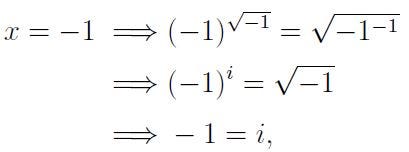
In contrast, x = 1 and x = 4 are valid solutions.

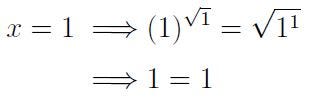
Lastly, we consider:

The value of 0^0 remains a topic of debate; some argue it is undefined, while others claim it equals 1. I view it as undefined, so I do not consider x = 0 a valid solution. Thus, the only confirmed solutions are x = 1 and x = 4.

I hope you found these problems enjoyable and perhaps gained insights or practiced valuable techniques. While these may not be groundbreaking, familiarity with such methods fosters a deeper understanding of mathematical values and expressions, ultimately aiding in tackling more complex questions.

Thank you for reading! I would greatly appreciate your support by following me and my publication, Y(Math), to help broaden my audience. If you’re interested in contributing to Y(Math), please share a draft with me at [email protected]. I would love to welcome more writers!

Video Resources

To further assist in your understanding, here are two relevant videos:

The first video, GED Math Test 2021 (7 NO CALCULATOR Practice Test Questions) PART 3, provides an excellent overview of non-calculator math questions, encouraging practice and skill enhancement.

The second video, GED Math No Calculator No Problem! A Practice Test to Help You Pass Faster!, focuses on strategies and tips for solving math problems without a calculator, ideal for reinforcing your learning.